하쿠's 강화학습 :: [Ch. VI] Temporal-Difference Learning
포스팅에 앞서 이 게시글은 Reference의 contents를 review하는 글임을 밝힌다.
「Temporal-Diffence Learning(TD학습)」
'Temporal-Difference Learning(이하 TD학습)'은 강화학습에서의 가장 핵심적인 아이디어라고 말할 수 있다.
TD학습은 이전 포스트들에서 배운 DP와 MC의 장점들을 혼합하여 만든 방법이다.
아래의 표를 보자.
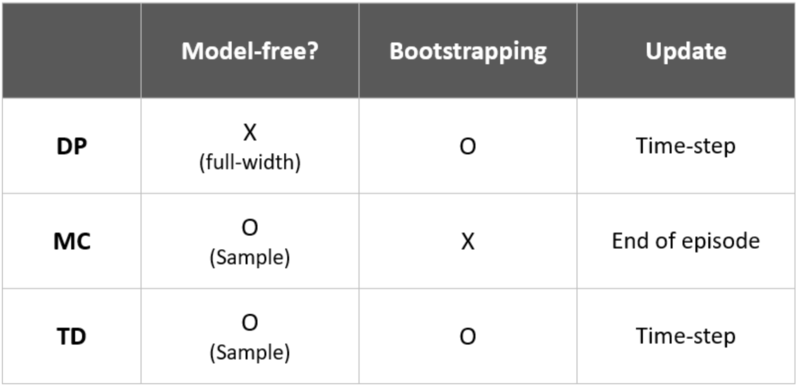
표에서 1번째 컬럼은 "환경에 대한 정보에 대해 완전히 알고 있는가?"에 대한 속성이다.
이전에 설명했다시피, DP는 환경에 대한 완전한 정보를 가지고 평가를 통해 계획을 세우는 'Planning'이라고 하였다.
반면, MC는 환경에 대한 불완전한 정보를 가지고 예측을 통해 학습하는 'Learning'이라고 하였다.
TD는 MC와 같이 환경에 대한 완전한 정보 없이도 진행이 가능한 'Learning'의 한 종류이다.
이어서, 2번째 컬럼은 "Bootstraping(이하 부트스트래핑) 방식을 사용하는가?"에 대한 속성이고 3번째 컬럼은 "갱신 시점이 언제인가?"에 대한 속성이다.
Bootstraping(부트스트래핑)
여기서 잠깐 'Bootstraping'에 대해 간략히 설명하자면, 이것의 정의는 "통계학에서 임의의 샘플링을 대체와 함께 사용하는 테스트 또는 메트릭이며, 더 광범위한 재샘플링 방법에 속한다"이다. 부트스트래핑을 활용할 때, 기저에 있는 아이디어는 모집단에 대한 예측이 샘플 데이터를 재샘플링하고 재샘플링 데이터에서 샘플에 대한 예측을 수행함으로써 모델링 될 수 있다는 것이다.
예를 들어 N번째의 예측치를 가지고 N+1번째의 예측치를 구성하게 되면, N+1번째의 예측치를 가지고 전체 모델(최적의 정책)을 예측하는 목표를 달성할 수 있다는 뜻이다. 이해를 돕기 위해 식을 살펴보도록 한다.
이전에 살펴보았던 강화학습에서 활용하는 증분 형태의 평가식을 떠올려보자.
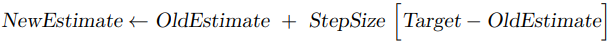
위와 같은 식에서 Target 부분에 Return(반환값)이 들어가면, Monte Carlo Method의 예측값을 갱신하는 식이었다.
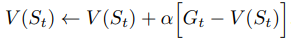
반면 Target 부분에 Value Function(다음 상태의 가치함숫값)이 들어가면, Temporal-Difference Learning의 예측값을 갱신하는 식이다.

보이는 것처럼 TD는 갱신의 목표점이 다음 상태에 대한 가치함숫값인데, 이는 이전 에피소드까지의 예측식을 활용한다.
이와 같은 방식을 'Bootstraping(부트스트래핑) 방식'이라고 하며 이는 실시간으로 값을 갱신할 수 있다는 점이 장점이다. DP 역시 이 같은 방식을 쓰지만 MC는 에피소드 진행 시 발생하는 샘플(학습 데이터)을 가지고 학습하며, 에피소드가 종결된 후 갱신하는 방식이었기 때문에 위의 표와 같이 표기되었다.
돌아와서 TD에서는 다음 상태(V(St+1))의 가치에 대한 이전 샘플(N-1번째 정책(과거) 기반)과 현재 상태의 가치에 대한 이전 샘플(N-1번째 정책(과거) 기반) 차이를 활용하여 Step size(=Learning rate)만큼의 반영비를 곱하여 새로운 현재 상태 가치 샘플을 만들어 낸다.
이때 이러한 차이를 'Temporal Difference Error(이하 TD 오차)'하며, 이렇게 다음 상태에 대해 이전 가치평가를 기준으로 구하여 이를 갱신식의 목표(최적정책 추론)로 삼아 현재 가치함수를 평가하고 새 정책을 구성하는 알고리즘을 'Temporal Difference(TD) 알고리즘'이라고 한다. 이 알고리즘의 버전에는 여러 가지가 있지만, 방금 살펴본 것은 TD(0) 또는 One-Step TD라고 불리는 알고리즘이다. 이는 바로 다음 상태의 가치(V(s+1))만을 고려하여 결정을 내려서 이름 붙여졌다..
다음은 TD 알고리즘을 설명할 때, MC 알고리즘과의 차이를 명확히 구분하기 위해서 자주 쓰이는 예시이다.
예시) 퇴근길

위의 표는 퇴근길 과정을 표로 정리한 것이다.
Elapsed Time = 실 소요시간
Predicted Time to Go = 도착까지 남은 시간에 대한 예측
Predicted Total Time = 총 소요시간에 대한 예측
이 표를 보고 아래의 그래프를 보면, 각 알고리즘 별 해결방법의 차이를 확연히 알 수 있다.

좌측은 Monte Carlo Prediction, 우측은 Temporal-Difference Prediction에 의해 예측한 방법을 그래프로 나타낸 것이다.
MC 예측은 최종적인 경과시간에 대해 처음부터 지향점을 두고 예측을 해나간다. 그때그때 샘플 값의 노이즈에 따른 변동은 보이나, 결론적으로 여러 모든 시점에서 하나의 전지적인 예측값을 보고 갱신해나간다.
반면, TD 예측은 각 시점에서 다음 상태까지의 데이터를 가지고 제한적인 예측을 해나간다.
바로 다음 상태까지만 고려하여 지향점을 바꾸기 때문에 시점에 따라 최종 값 예측에 대한 변동폭이 크다.
한마디로 MC 방식은 장기적인 비전을 가지고 수행하는 반면, TD 방식은 그때그때 임기응변식의 대처를 통해 비전에 대한 변동 반영이 돋보이는 방법이다. 이 문장만 보면 MC가 우수한 방법인 것 같으나, TD는 다음과 같은 장점들 때문에 가장 대중적으로 쓰이는 방법이 되었다.
「Temporal-Difference Prediction(TD 예측)의 장점」
여기서는 MC와 DP대비 TD의 장점을 알아보도록 하겠다.
이후 포스트에서도 간간히 등장하겠지만, 우선적으로 TD의 장점이라고 할 수 있는 부분들은 다음과 같다.
1. 불완전한 모델에 적용 가능(DP 대비)
2. 실시간 가치함수 갱신(MC 대비)
TD는 DP와 다르게 'Model-Free 한 환경(불완전한 학습정보)에 적용이 가능'하다. 이는 강화학습을 실제 환경에 적용이 가능한가 하는 문제로 중요하다고 할 수 있다. 또한 TD는 DP에서 활용되었던 테이블 방식의 문제 해결뿐만 아니라 선형 함수를 통한 근사화 문제에도 적용 가능하다(이에 대해 추후 게재할 예정).
같은 Model-Free 한 환경에서의 학습법인 MC와 비교해서는 '실시간 가치함수 갱신이 가능'하다는 점이 우수하다.
역시, 실제 환경에서는 실시간으로 환경과 상호작용을 할 수 있어야 하는데 그러한 면에서 TD가 MC보다 낫다.
추가적으로 TD는 MC와 동일하게 점근적 발전을 통해 종국에 최적정책으로의 수렴을 보장하기 때문에 성능면에서도 뒤처지지 않아 좋은 알고리즘으로 평가받는다.
추가적으로 TD는 학습 속도와 제한된 학습여건(제한된 데이터량)에서의 효과가 뛰어나다.
학습 속도의 경우, 수학(이론)적으로 아무도 아직까지 입증하지 못하였으나(아직까지 어떤 과제에 대해 적합한 알고리즘이 TD냐 MC냐에 대한 기준도 명확하지 않은 상태), 경험적 측면에 근거하여 실전에서 TD가 MC에 비해 조금 빠른 수렴(학습) 속도를(학습) 보인 것으로 나타났다.
MC는 기본적으로 에피소드가 종결한 뒤에 추출 가능한 Return(반환값)을 기준으로 학습하지만, TD는 Bootstraping방식을 활용하기 때문에 제한된 학습여건 속에서도 강력한 알고리즘이라고 할 수 있다.
「Temporal_Difference(0, One-step)의 최적화」
TD는 기본적으로 MC 방법의 적용에 한계를 느끼는 무한히 길어질 수 있는 에피소드에서도 작동 가능한 방법이라고 했다.
제한된 경험(샘플데이터)을 가지고 점진적 학습을 이어나가는 학습법들의 공통점은 그러한 경험들을 학습이 완료(수렴)될 때까지 지속해서 제시하는 점이다.
이러한 방법이 가능한 데에는 'Batch updating'방법이 가능하기 때문이다.
Batch updating은 우리가 한 번의 학습 시 학습 가능한 데이터에 대해서만 학습하는 경우를 말한다(딥러닝에서 사용되는 그것이 맞다).
이를 강화학습에서의 예시를 들자면, 무한대에 수렴하는 Step이후에 에피소드가 종결되는 루틴을 가진 환경에서는 전체 환경에 대한 정보(경험)를 다 얻으려면 학습루틴이 무한히 길어질 수 있으므로, 일정 시점(일부 정보)까지의 경험을 저장하고 이를 토대로 부분 갱신을 하는 방식이다.
이는 즉 갱신의 과정에서 각 시점에서의 예측마다 갱신하는 방식으로서 이후, 이를 반복적으로 수행해 최종 결과(Global Optimum)에 도달(수렴)하게 하는 것이다.
같은 방법으로 제한된 환경 내의 MC 역시 활용할 수 있다만, 아래와 그림과 같이 TD와의 성능 차이를 보인다.
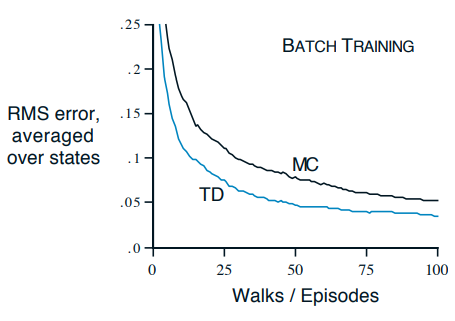
이런 결과를 보이는 이유는 MC는 정확한 반환값을 기반으로한 방법인데, 반환값 자체에 대한 정확한 평가가 성립되지 않아 이후 개선에서 한계를 보이는 것이다.
이와 반대로 TD는 이전 정책을 통해 예측한 가치함숫값을 토대로 사용하는 진행방식인 최대 우도 모델 추정(Maximum-likelihood Estimation)이기 때문에, 훨씬 더 성능이 좋다.
최대 우도 모델 추정(Maximum-likelihood Estimation)
최대 우도 모델 추정은 통계학에서 밝혀낼 대상이 되는 미지의 모델의 확률분포에서 뽑은 표본 데이터를 중심으로 모델을 추정하는 방식이다.
반면 MC는 이전의 경험을 활용하지만 이전 정책을 기반으로 하는 방식이 아니고 지속적으로 공급되는 경험을 통해 새 정책을 구성한다는 점에서 최대 우도 모델 추정이 아니다.
그렇다면 한 가지 의문이 생기는데, "그래서 이러한 특징이 무슨 차이를 만들어내는가?"이다.
방금 언급했던 최대 우도 모델 추정은 결국 앞서 언급했던, Bootstraping을 활용하는 추정방식이라고 할 수 있다.
이러한 방식이 만들어내는 차이를 설명하기 위해서는 확실-등가 추정(Certainty-Equivalence Estimation)이란 개념이 필수적인데, 이는 Bootstraping 방식의 특성에 대한 설명이다.
확실-등가 추정(Certainty-Equivalence Estimation)
확실-등가 추정은 '미지의 A모델에 대해 Bootstraping 추정 방식에 의거 특정 B 모델을 추출(평가결과 모델)하게 되었다면, B 모델은 A모델에 대한 확실성을 가지고 있다는 추정'이다.
확실-등가 추정은 위 그림에서 TD가 MC보다 더 빨리 수렴되는 이유를 설명한다. 왜냐하면 TD가 구성하는 정책에 대하여 확실성을 갖는다는 전제하에 불필요한 연산을 줄이고 평가와 개선을 이어나가기 때문이다.
이러한 방식은 편향(Bias)이 발생할 가능성이 있지만, 속도가 훨씬 빨라진다.
이러한 원리에 의해 TD가 MC에 비해 제한된 환경(연속적 과제) 내에서 보다 좋은 성능(뛰어난 적용성과 속도)을 보인다.
「SARSA = Online-Policy(On-Policy) TD Control(살사)」
On-Policy 기반의 TD제어방법인 'SARSA'에 대해 알아보겠다.
SARSA는 State, Action, Reward, next State, next Action순서로 진행되는 시퀀스 구성요소들에서 한 글자씩 따와 명명한 것이다.
기본적으로 GPI방식을 기반으로 하며, 행동가치함수(상태-행동 쌍) 기반의 알고리즘이다. 아래와 같은 식을 사용한다.
행동에 대한 'A_t+1' notation은 현 정책에 따라 선택된 다음행동의 행동가치함숫값을 사용한다는 의미를 지닌다.
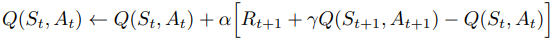
이 갱신식은 종점이 아닌 상태 St에 대해서만 적용이 가능하며, 기본적으로 종점의 행동가치함숫값은 ‘0’으로 고정이다.
SARSA의 다이어그램은 이와 같이 표현할 수 있다.
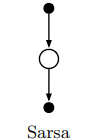
아래는 SARSA 방식의 평가를 의사코드로 나타낸 것이다.

이를 보면, 갱신의 목표점인 Target에 위치한 값이 정책에 의해 선택된 다음 상태의 Q(행동가치함숫값)를 기준으로 갱신된다는 것을 알 수 있다.
이에 대해 부연설명을 하자면, SARSA는 현재 상태St의 Q와 다음 상태St+1의 Q를 선택함에 있어서 정책기반의 E-greedy 또는 Greedy 알고리즘을 활용할 수 있는데, 전자의 경우 E(불확실성)에 의해 학습수렴속도가 늦어진다는 단점이 있고 후자의 경우에는 Local Optimum에 빠질 수 있다는 단점이 있다. 정리하면, 아무래도 현 정책에서 행동선택과 이를 따르는 방식의 갱신을 진행하는 만큼 어느 정도 편향(Bias)이 있는 것이다.
「Q-learning, Offline-Policy(Off-Policy) TD Control(Q-러닝)」
Off-Policy 기반의 TD 제어방법인 'Q-learning(이하 Q-러닝)'에 대해 알아보겠다.
Q-learning 역시 GPI방식을 기반으로 하며,행동가치함수(상태-행동 쌍) 기반의 알고리즘이다. 다만 아래와 같은 갱신식을 사용하는데,

오프폴리시의 특징대로, 행동선택과 Target값 선정에 있어 정책(Target Policy)과 무관하게 탐험정책(Behavior Policy)을 기반으로 최적정책(Optimal Policy←Target Policy)을 구성하는 부분과 최대 Q(최대행동가치함숫값)를 타겟으로 잡아 학습한다는 부분이 특징이다.
아래는 Q-learning 의사코드이다.

이를 보면, 갱신의 목표점인 Target에 위치한 값이 정책과 무관하게 다음 상태에서의 최대 Q(최대행동가치함숫값)를 기준으로 갱신된다는 것을 알 수 있다. 또한, 이러한 방식은 온폴리시 방식보다 편향(Bias)이 적다.
아래는 Q-learning의 다이어그램이다.
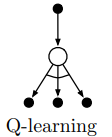
SARSA vs Q-learning
그렇다면 SARSA와 Q-learning 중에서 "어느 알고리즘이 더 우수한가?", "어떠한 측면에서 차이점을 보이는가?"와 같은 의문점이 생길 수 있다.
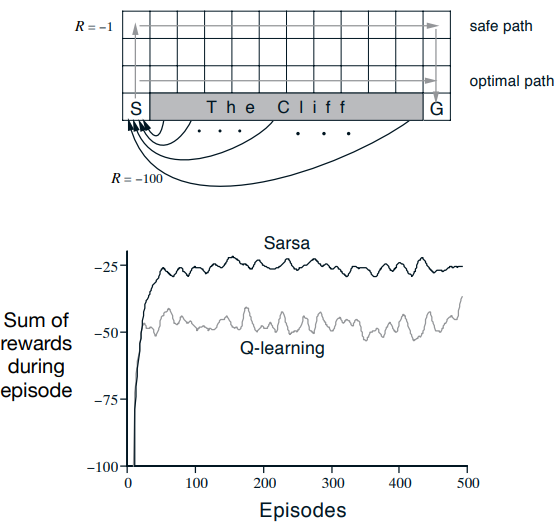
이를 비교하기 위해, 'Cliff'라는 환경을 기반으로 비교를 진행할 것이다.
우선 이 과제는 시점과 종점 그리고 절벽(Cliff)이 있다. Cliff로 향하는 행동에는 -100의 보상이, 이외의 행동에는 -1의 보상이 주어진다. 목표는 Cliff를 피해 시점에서 출발하여 종점까지 보상을 최대화하는 최적의 경로를 찾는 것이다.
위의 그래프들을 들여다보면, 두 알고리즘 간의 차이를 확인할 수 있다. 우선 상단의 그래프는 환경지도를 나타낸다.
하단의 그래프를 보면 성능 차이를 실감할 수 있는데, 이는 SARSA와 Q-learning의 근본적인 방법론 차이에 있다.
SARSA는 Target에 의거한 갱신식의 형태가 현 정책에 기반하여 다음 상태의 행동가치의 평균치를 고려하는 방식이다. 이것은 Cliff 근처 지점의 상태에 대해서 상당히 비관적인 가치평가를 한다(Cliff로 빠지는 행동가치함숫값에 의해 상쇄가 발생). 따라서 이는 Cliff로부터 비교적 가장 먼 거리의 상태(정책에 따른 전체적 행동가치함숫값이 높은 상태)들을 위주로 경로를 짜게 만들고, 결론적으로 Safe path라고 불리는 경로를 형성하게 한다.
반면, Q-learning은 Target에 의거한 갱신식의 형태가 정책과 무관하게 다음 상태의 최대행동가치를 고려하는 방식이다. 이것은 주변 상태로서 Cliff가 존재하는지의 여부와 관계없이 오로지 최대가치행동만 보기 때문에 이를 가진 상태(최대행동가치함숫값을 가진 상태)들만 한 곳에 모아, 최단 거리 경로인 Optimal path를 구성하게 된다.
「Expected SARSA(기댓값을 활용한 SARSA)」
앞서 살펴보았듯, 결국 SARSA와 Q-learning의 차이는 갱신식의 'Target'의 차이였다. 현재 정책에 따라 계산한 행동가치함숫값을 목표로 삼는 갱신을 추구하면 SARSA, 정책과 무관하게 최대행동가치함숫값을 목표로 삼는 갱신을 추구하면 Q-learning이었다.
이처럼 타겟을 변형하면 다른 알고리즘이 등장하게 되는데, 그중 하나가 'Expected SARSA(기댓값을 활용한 살사) 알고리즘'이다.
Expected SARSA는 아래와 같이 이제까지의 갱신식에서 타겟을 다음 상태-행동 쌍에서의 기댓값(다음 행동가치함수들의 평균)으로 바꿔주고, 예외의 상황에 대한 갱신식은 최대행동가치기준 갱신(Q-learning 방식)을 한다. 이 또한, On-Policy형태와 Off-Policy형태 모두 구현할 수 있으나, 여기서는 On-Policy형태로 소개할 것이다.
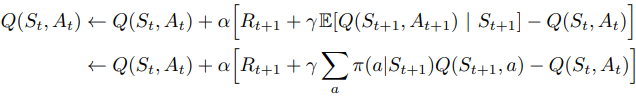
앞서 살펴보았던 Cliff Task에 대해 Sarsa와 Q-learning보다 더 우수한 성능을 보이는데, 지금부터 우수한 부분들을 설명해보겠다
(다만, 모든 Task에 대해 두 알고리즘보다 우수하다고 단정할 수는 없다).
Expected SARSA는 다음과 같은 이유로 이전의 두 알고리즘보다 강력한 성능을 보이는데,
1. 무작위적 다음 행동선택에 대한 분산 감소로 인한 성능 향상
2. Step size(Learning rate)가 커도 무관
우선 1번은 SARSA의 단기적 성능 저하의 주 원인인데, 다음 상태에서의 행동에 대한 무작위성 때문에 Target이 흔들려 이에 갱신 성능이 저하된다. 하지만, 전체적인 행동가치함숫값의 평균치를 고려하여 갱신을 이어나가는 Expected SARSA는 비교적 Target의 분산이 적어, 그로 인한 비효율적 갱신의 부담이 줄게 된다.
2번은 1번과 같은 맥락에서 SARSA는 초기 정책에 대한 편향이 노이즈로 잡혀있어 위험성이 있다는 단점 또한 있는데, Expected SARSA는 초기에 잘못된 방향으로 형성될 가능성이 있는 정책으로부터의 영향력이 SARSA보다 비교적 적기 때문에 학습률인 Step-size를 크게 잡아도 무관하게 성능이 증가한다. Expected SARSA의 이러한 부분들은 경험이 제한적인 환경에서도 용이하게 쓰일 수 있다.
책에서는 Q-learning 대비 우수성을 직접적으로 언급하지 않았으나, 기본적으로 예외의 상황에서는 Q-learning의 틀을 활용하고 평소에는 기댓값(반환값, Target으로의 최적의 값)을 활용한다는 측면에서 자연스레 Q-learning보다 우수한 성능을 짐작할 수 있다(아래의 성능 그래프 역시 이를 잘 보여준다).
아래는 세 알고리즘의 성능 비교이다.
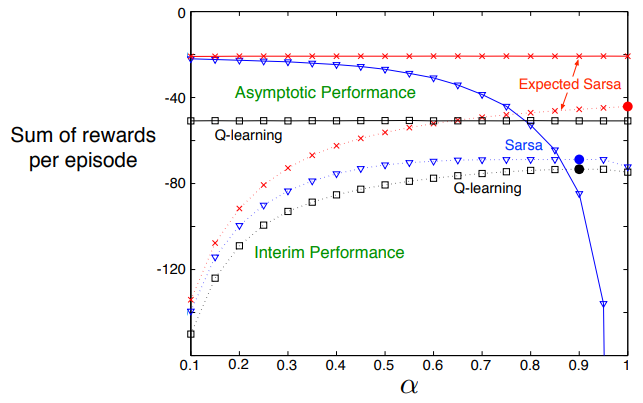
그래프를 보면 알 수 있다시피, 점근적 퍼포먼스 향상과 훈련 중간 퍼포먼스 모두 해당 과제에 대해 Expected SARSA가 우위를 점하는 것을 알 수 있다.
「Maximazation bias and Double learning(최대화 편향과 이중 학습)」
Maximazation bias(최대화 편향)
'Maximazation bias(최대화 편향)'이란?
강화학습의 목표인 보상에 있어서 값의 차이를 보이지 않을지라도, 더 나은 가능성(양+의 미래 보상에 대한 추종에 의해 해당 방향으로 학습이 치우쳐지는 현상을 말한다.
아래의 그림을 보자.
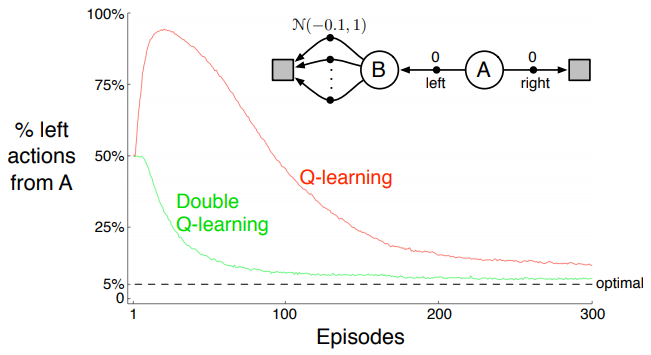
우선 Task에 대해 설명하자면, 시작 State는 A이다. A에서 우측방향 선택 시 종료지점으로 곧장 이동하나, 이에 대한 보상은 '0'이다. 이와 반대로 좌측 선택 시 상태 B(종결 지점의 직전 지점)로 이동한다. B는 종결 지점은 아니고 이동에 따르는 보상 역시 '0'값으로 동일하게 주어지지만, 다음 상태에서의 다음 행동에 대한 보상이 평균 –0.1 값을 기준으로 분산이 1인 범위 내에 수많은 행동으로 구성되어있다. 이러한 환경(Task)에 놓여있을 때, 과연 어떤 수가 최적의 수일까?
평균값이 –0.1이기 때문에 사실상 좌측으로 가는 행동 자체가 오류일 수 있다(리스크를 떠안고 있기 때문). 하지만, 우리의 알고리즘은 좌측을 선호한다. 그곳에 '더 나은 보상에 대한 가능성'이 있기 때문이다.
위와 같이, 사실상 B 상태의 즉각 보상과 A 상태의 즉각 보상의 차이가 없더라도 더 나은 가능성(양+의 미래 보상에 대한 가능성)에 의해 한쪽으로 치우쳐지는 현상을 'Maximazation Bias(이하, 최대화 편향)'이라고 한다.
강화학습에서는 이러한 편향을 생기는 원인 중 하나로 '훈련 시 하나의(같은) 샘플을 활용해 모델을 사용하는 부분'을 꼽았다. 하나의 샘플에 대한 모델은 결국 그 데이터 양이 한정(탐험 부족)될 경우, 편향(Bias)이 생길 가능성이 높기 때문이다.
따라서 이를 해결하기 위해, 'Double learning or Doubling(이중 학습)'의 개념이 등장하게 된다.
Double learning or Doubling(이중 학습)
샘플을 2개의 부류로 나누고 이에 대한 각각의 예측을 진행하여 Q1, Q2(모델, 행동가치함수)를 만든다. 이에 대해, Q1에서 예측한 최대가치행동의 행동가치값을 Q2에서 추출 또는 Q2에서 예측한 최대행동의 행동가치값을 Q1에서 추출하는 방식으로 연산에 사용하면 편향(Bias)을 줄일 수 있다고 생각했는데, 이러한 방법이 Maximazation Bias를 제거할 해결책으로 고안된 'Double learning or Doubling(이중 학습)'이다.
이중 학습을 활용하면 각 샘플에 대한 종합적인 결과를 기반으로 모델을 추정할 수 있는데, 쉽게 말해 같은 대상에 대한 탐구를 조사 인원이 하나의 조사자료를 바탕으로 검증하는 것이 아닌 조사 인원별로 각자의 조사자료를 연구하여 추후 논의를 통해 조율해나가는 방식이라고 이해하면 편할 것이다. 조율(평균화)하는 과정에서 노이즈(편향)가 사라질 것이기 때문이다.
아래는 이중 학습의 갱신식이다.
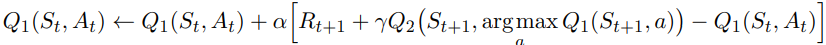
위 갱신식은 Q1모델에서 최대가치행동을 선정해 이를 Q2모델에서 수치 추출하는 방식으로 Q1모델을 갱신하는 식이다.
이는 역순으로 활용이 가능하며, 이 예측치는 결국 두 방법 중 어느 쪽을 써도 종국에는 최적의 행동가치함숫값으로 수렴한다는 점에서 편향되지 않는다(Unbiased). 여기서 반드시 기억해야 할 점은, 두 가지 예측치를 사용하지만, 하나의 예측치만 갱신된다는 점이다.
결론적으로 Double learning은 메모리 요구사항을 2배로 증가시키는 부분은 있지만, 계산량은 증가시키지 않는다.
아래는 Doubling을 활용한 Q-learning의 의사코드이다. 이는 절반의 확률로 Target Policy를 전환하고, 그에 따른 예측치 갱신도 하고 있다.

이중 학습은 추후 여러 알고리즘에서 옵션처럼 사용되는 기법이므로 잘 기억해둬야한다.
「마무리」
이번 장에서는 새로운 학습법인 TD를 배웠다.
DP와 같이 Bootstraping 방식을 활용하여 적용성을 높였으며, MC를 대체할 수 있는 Learning(학습법)이다.
GPI방식에 기반을 둔다.
TD는 행동선택에 있어서 현 정책에 대한 의존 여부에 따라, On-Policy방법과 Off-Policy로 나뉜다.
이 둘의 차이는 탐험에 대한 보장 정도와 그로 인한 편향 정도이다.
TD는 오늘날 대중적으로 쓰이는데, 아래와 같은 장점이 있기 때문이다.
1. 간편함, 간단함과 그로 인한 연산량 최소화
2. 실시간 방식, 환경과의 상호작용을 통한 샘플(학습 데이터) 생성
갱신의 목표점이 되는 Target을 바꾸면 다양한 형태로 응용이 가능한데, 이로 인해 최신 알고리즘들의 근본 현재 상용화되고 있는 알고리즘들 중에는 TD의 파생형이 많으며, 그들은 TD-error에 갱신을 맡기고 있다.
이번장에서 알아본 TD는 정확히 One-step, Tabular, Model-Free 방법이다.
다음장에서는 N-step TD에 대해 알아볼 예정이고, Model-Based환경(DP)에서 활용하는 법과 이후 Approximation을 위한 다양한 함수 형태의 해결책을 만나볼 것이다.
「참고」
Reinforcement Learning, Second Edition : An Introduction
Richard S. Sutton and Andrew G. Barto
https://mitpress.mit.edu/books/reinforcement-learning-second-edition
Reinforcement Learning, Second Edition
The significantly expanded and updated new edition of a widely used text on reinforcement learning, one of the most active research areas in artificial intelligence. Reinforcement learning, one of the most active research areas in artificial intelligence,
mitpress.mit.edu