하쿠's 강화학습 :: [Ch. VII] n-step Bootstrapping
포스팅에 앞서 이 게시글은 Reference의 contents를 review하는 글임을 밝힌다.
「n-step Bootstrapping(n단계 부트스트래핑)」
이번 포스트에서 살펴볼 개념은 'n-step Bootstrapping(n단계 부트스트래핑, 이하 n-step)'이다.
n-step은 기존 TD 방식이 바로 다음 미래(one-step)만을 고려함으로써 가지는 제약을 해결하기 위해, n단계 미래까지 고려하는 방법이다. 이것은 하나의 알고리즘이 아니라 존재하는 알고리즘(TD)에서 추가할 수 있는 특성과 같다고 생각하면 편하다.
이미 눈치챈 사람도 있겠지만, n-step TD 방식은 여러 단계를 고려하는 방법이라는 점에서 모든 단계를 고려하는 MC와도 공통점이 있다. 하지만, MC와의 차이점은 n-step TD 방식은 모든 단계를 고려하지 않는다는 점이다.
다시 말해, n-step을 활용한 TD는 일반 TD(one-step)과 MC의 절충 형태의 알고리즘이라고 할 수 있다.
우선 이전에 배웠던 알고리즘들에 대해 가볍게 되돌아보자.
MC는 철저히 Episodic Task에서 활용 가능한 방법으로 필히 에피소드가 종결되어야 예측 및 평가가 가능했다. 또한 이러한 예측과 평가는 전 단계(Trajectory)에 영향을 끼치므로 초기 정책에 대한 편향(Bias)이 적고 그로 인해 처음부터 Global Optimum으로 수렴의 방향을 잡지만, 분산이 크다는 단점이 있었다.
반면, TD는 실시간 갱신이 가능하여 Continuous Task(↔Episodic)에서도 빛을 발하지만, 바로 다음 상태만 고려가 가능하기 때문에 비교적 MC보다 편향(Bias)이 크다는 단점(그때그때 Global Optimum에 대한 예측이 달라진다)과 그럼에도 각 시점에서의 정책에 기반하여 Global Optimum을 추적하기 때문에 분산이 작다는 장점이 있었다.
각각의 알고리즘은 예측과 갱신의 측면에서 양극단에 걸쳐있다고 할 수 있는데, 이러한 차이는 결국 '바라보는 단계 수의 차이'에서 오는 것이었다. 특히나 TD는 그것의 메커니즘적 측면에서 중요한 이벤트가 발생한 경우에 대한 반영이 중요한 방법론인데, one-step의 경우 고려하는 미래 시점이 1단계뿐이기 때문에 이러한 이벤트가 갱신식에 포함될 확률이 n-step에 비해 낮다(쉽게 말해 one-step TD는 근시안적이기 때문에 가까운 미래에 존재하는 종결 상태에 대한 최적화 반영이 n-step에 비해 떨어진다는 뜻).
정리하면 MC와 one-step TD를 각각을 '정'과 '반'으로 보았을 때, '합'에 해당하는 알고리즘이 바로 이 'n-step'을 활용한 알고리즘이다.
아래는 이러한 차이를 보여주는 그림이다.

「n-step TD Prediction(n-step TD 예측)」
n-step TD는 2단계 이상이면서 총보상(반환값) 미만 즉, n-1단계 이하의 보상까지를 고려하여 예측과 갱신을 하는 알고리즘들을 말한다.

또한 n-step TD는 one-step TD의 파생형인만큼 그것의 갱신식 Target을 변환해주어 갱신식을 도출할 수 있는데, 갱신의 목표인 Target을 각 시점에서의 n단계 앞까지의 보상값들의 합으로 즉, 다시 말해 n단계 미래 보상까지의 축적값을 목표로 갱신한다(이것은 총보상의 일부분이라고 할 수 있다).

아래는 n-step TD 예측을 의사 코드로 나타낸 것이다.

추가적으로 n-step TD 알고리즘의 오차(error)와 관련하여, 'Error reduction property(오차 감소 속성)'이라는 것이 있는데, 이는 다음의 부등식을 만족하는 속성으로 n-step TD방법을 사용하면 n-step 이후의 상태가치에 대한 최악의 평가값보다 Discount factor의 n제곱 배만큼의 적은 에러를 보장할 수 있다는 법칙이다. 원리를 이해하는 데에 도움 삼아 알아두도록 하자.

다음은 어떤 Task에 대한 MC와 one-step TD 그리고 n-step TD의 전체 진행 대비 초기 정책의 성능을 비교한 것이다.

x축은 step size, y축은 error을 나타낸 것인데, 확실히 n-step TD가 다른 두 방법에 비해 초기 성능이 우월함을 알 수 있는데, 결국 이것은 더 빠른 속도로 최적의 학습에 수렴이 가능하다는 것을 나타낸다.
「n-step SARSA = n-step Online-Policy(On-Policy) TD Control(n단계 살사)」
이번에는 이러한 n-step TD의 제어방법에 대해 알아볼 것이다.
먼저 On-Policy TD제어 방법인 SARSA에 n-step을 적용해볼텐데,우리는 이것을 'n-step SARSA'라고 한다. 아래의 갱신식을 같이 보자.

이것은 n-step SARSA의 반환값이다. 현재 시점에서 미래(지연) 보상들을 감가한 값과 n-step 후에 도달하는 상태를 감가한 값을 합해주고 있다.

이것은 갱신을 위한 증분 형태의 가치함수 갱신식인데, 보다시피 갱신의 목표인 Target값이 행동에 따른 즉각보상 R에서 n-step에 걸친 반환값으로 바뀌어 있다. 이것은 결국 n-step 뒤에 출현할 행동가치함숫값(정책기반)을 함께 고려하겠다는 뜻이다. 이것이 n-step SARSA이다.
아래는 n-step SARSA의 다이어그램이다.

다이어그램을 보면 TD와 MC 그리고 그것의 절충점인 n-step TD의 형태를 볼 수 있다.
다음 예시는 G를 향한 길찾기 과제에 대해 1회 학습 직후, one-step SARSA와 n-step SARSA의 학습을 비교한 것이다. 보상은 종결 지점으로 가는 행동에 대해서만 주어지고 나머지 상태-행동 쌍에 대해서는 '0'으로 고정되어있다.

보이다시피 one-step SARSA의 경우, 종결 직전 상태에서의 1가지 행동에 대해서만 학습하였다(one-step).
반면 n-step SARSA의 경우, 종결에서부터 n단계 이전까지의 상태-행동 쌍에 대해 학습이 가능하였다.
즉, 적은 에피소드 수에서 보다 효과적으로 학습할 수 있는 것은 n-step 방식이라는 것이다.
Expected SARSA
여러 SARSA의 step별 종류를 나타낸 표에서 우측 끝의 n-step Expected SARSA의 경우, 이전 포스트에서 배운 것과 원리는 동일하다.
Expected SARSA의 다른 모든 것은 SARSA와 동일하고 마지막 행동가치선택에 있어 정책에 기반한 행동가치의 평균치 즉, 상태가치함숫값을 Target으로 삼은 갱신식을 사용했었다.
여기서는 추가적으로 n-step옵션만을 더해서 생각해주면 된다.

n-step Expected SARSA의 경우, Target값으로 선택할 반환값 계산에 있어서 정책에 기반한 행동가치함숫값의 평균치를 사용하면 된다.
다시 돌아와서, 아래는 지금까지 언급했던 n-step SARSA의 의사 코드이다.

「 ??? = n-step Offline-Policy(Off-Policy) TD Control × 중요도 샘플링 활용」
이전 포스트에서 On-Policy와 Off-Policy가 서로 대응되며 SARSA와 Q-learning이 각각의 알고리즘으로 소개된 바 있었다.
따라서 앞서 n-step을 속성을 포함한 SARSA가 'n-step SARSA'였던 것과 같이 Off-Policy Control의 경우 'n-step Q-learning'이라고 단순 추측을 할 수 있겠으나, 실상은 그렇게단순하지 않다.
우선, 우리는 이전 포스트(Monte Carlo Method)에서 Off-Policy를 다룰 때 'Importance Sampling(이하 중요도 샘플링)'에 대해서 알아보았다.
중요도 샘플링은 결국 "내가 얻은 샘플이 내가 구하려는 최적에 얼마나 부합하는가?"를 나타낸 것이었다.
중요도 샘플링 개념이 다시 등장하는 이유는 n-step TD의 경우 MC방법과 같이 Trajectory기반의 반환값을 Target으로 사용하기 때문이다.
이를 설명하기 위해 MC 방법의 경우를 좀 더 들여다보면, MC는 실제 데이터 기반의 갱신을 진행하기 때문에 TD방법에 비해 다소 분산은 클지라도 편향이 적고 항상 Global Optimum의 방향으로 수렴한다는 장점이 있었다.
다만, TD와 다르게 샘플(학습 데이터)이 하나의 값이 아닌 Trajectory였기 때문에 이것이 최적의 Trajectory와 얼마나 차이가 있는지를 보기 위해 비율(중요도 샘플링)을 계산하여 이를 예측에 반영하였었다.
이와 마찬가지로 n-step Off-Policy TD의 경우에도 Trajectory(t:t+n)를 학습 데이터로 활용하기 때문에 같은 방식을 적용할 수 있다. 이러한 방식은 행동 선택 시에 무작위적으로 행하는 Behavior Policy에서는 의미 있는(최적에 부합하는) Trajectory가 선택될 확률이 On-Policy의 경우보다 적기 때문에, 이러한 상황에서 적게 등장하는 최적의 경우에 대해 보다 효과적으로 학습하기 위해서이다.

이러한 중요도 샘플링 기법은 On-Policy의 경우, 항상 '1'이라는 것을 추측할 수 있다.
왜냐하면 모든 행동이 Target Policy에서 추출되고 그것이 곧 현재 정책이 지향하는 행동들이기 때문이다.
다음 식은 이러한 중요도 샘플링을 적용한 갱신식과 n-step Off-Policy TD에 대한 의사 코드를 SARSA를 통해 나타내었는데, 이는 다음과 같다. 추가적으로 n-step Off-Policy Expected SARSA 역시 아래와 같은 갱신식으로 나타낼 수 있다. 다만, 중요도 샘플링 비율의 중요성은 조금 떨어질 것이다.


「Control Variate(분산 조절)」
중요도 샘플링의 장점은 비교적 그 샘플의 중요도를 파악해 더 많이 배울 수 있다는 점이다.
반면 단점은 선택되지 않은 샘플에 대해서 그 비율을 계산할 수 없다는 점인데, 이는 곧 중요도가 '0'으로 책정되어 연산에 고려되지 않는 치명적인 위험성을 갖는다. 중요도가 '0'이 되어버리면, 반환값과의 곱 연산이 '0'이 되어버리고 이것을 갱신식의 Target으로 활용하게 될 경우, 학습의 분산이 커지는 단점이 있다.
이러한 중요도 샘플링의 맹점을 해결하기 위해서는 통계학적 접근법이 요구되는데 이것이 'Control Variate(이하 분산 조절)'이다.
분산 조절의 아이디어는 간단하다.
중요도가 낮거나 없는 샘플에 대해서는 기존 가치평가로부터 변화를 최대한 적게 하여전체 학습의 분산을 낮춰 학습 수렴 속도에 이점을 주는 방법이다.
글로만 보면 이해가 어려우니 아래의 수식을 보자.

수식을 보면 p(중요도 비율)만큼은 n-step 반환값을, 1-p(나머지 비율)만큼은 기존 가치평가에 기반하여 갱신을 자제하고 있다. 이러한 수식은 중요하지 않은 학습 데이터에 대한 불필요한 갱신을 제거하여 전체 학습의 방향에 대한 분산을 줄이는 방법이다.
아래는 이를 정리하여 다음과 같이 활용한다.

정리하면, 중요도 샘플링을 활용한 방안은 좋은 성능을 낼 수 있지만 높은 분산값에 의해 비교적 적은 step size를 사용하게 되고 이는 학습 수렴 속도에 악영향을 끼친다(갈 길은 먼데, 조금씩 학습해야 하는 딜레마). 이러한 측면만 보면 On-Policy에 비해 학습 속도가 떨어지고, 학습 데이터의 측면에서도 비교적 양질이 아닌 데이터에 대한 학습이 발목을 붙잡기 때문에 좋지 못한 방법이라고 생각할 수 있다.
하지만 분명한 것은 이를 개선할 수 있다는 점이다. 여기서 제시한 '분산 조절'이외에도 여러 가지 방법들이 존재한다(여기서 알아보지는 않겠지만).
「Tree-back up = n-step Offline-Policy(Off-Policy) TD Control(트리백업)」
앞서 중요도 샘플링을 활용한 n-step Off-Policy TD제어를 살펴보았다. 이번에는 중요도 샘플링 없이 하는 n-step Off-Policy TD제어에 대해 알아볼 것이다.
아래의 다이어그램을 보자.

그림을 보면 각 상태와 해당 상태에서 선택 가능한 행동들이 있고, 그중 중앙 라인(상태-행동 쌍)을 따라서 여러 스텝을 진행했다고 가정한다.
n-step(multi-step)에서 Off-Policy 형태의 알고리즘을 통해 갱신하는 방법은 선택 가능한 행동들을 모두 고려한 가치함수를 활용하는 것이다.
정확히는 모든 선택지를 고려하는 이러한 분기 형태를 하나의 Tree라고 보았을 때, Tree의 leaf(잎사귀 부분)의 노드들을 활용한 갱신인데, 선택된 행동을 제외하고 나머지 행동들에 대해 정책이 정하는 가중치(선택비)를 고려하여 Target으로 쓰는 알고리즘이고 이것을 'Tree-back up 알고리즘(이하 트리백업)'이라고 한다.
트리백업은 가중치가 쌓이는 방식으로 연산이 진행되는데, 예를 들어 첫 번째 선택된 행동의 가중치 비율은 그 행동으로 인해 등장하는 상태에서 선택 가능한 즉, 2차 행동선택단에서 적용된다.



같은 원리로 두 번째로 선택된 행동의 가중치 비율은 해당 행동의 결과로 등장하는 상태에서 선택 가능한 3차 행동선택단에 적용이 된다. 물론 이전 비율도 곱해진 상황에서 말이다.

이를 이용해 진행해나가는 과정은 1-step당 2단계로 이루어지는데, 행동을 통해 다음 상태로 가는 샘플(학습 데이터) 추출과정과 선택된 행동 이외의 나머지 행동들에 대한 정책기반의 예측값을 고려하는 과정이다.
정리해 이를 반환값 연산에도 적용시키게 되면 아래와 같은 식들을 도출할 수 있다.



마지막으로 이러한 Tree-back up의 식에서 예측 선택에 대한 불확실성을 제거하면 완전한 n-step SARSA와 반환값에 대한 식이 동일함을 확인할 수 있다.

아래는 Tree-back up 알고리즘의 의사 코드이다.

「n-step Q(σ) = Unified n-step TD Control(n단계 큐시그마)」
앞서 여러 n-step에 걸쳐 행동가치함수를 기반으로 최적을 찾는 알고리즘들을 알아보았다.
n-step SARSA는 모든 샘플(상태)에 대해 상태변환확률을 가지고 있고 Tree-back up은 샘플링 없이 모든 상태행동쌍에 대한 상태변환확률(예측값)을 가지고 있으며, n-step Expected SARSA는 마지막 상태를 제외하고 모든 샘플에 대한 상태변환확률이 존재한다. 마지막 상태는 Tree-back up과 동일하게 예측 기반의 상태변환확률을 가진다.
이러한 알고리즘들은 각 단계에 있어서 Target 식의 차이에 따라 결과에 약간의 차이를 가질 뿐, 큰 틀에서는 상당히 유사하다. 그렇다면, 이들을 혼합한 형태의 알고리즘이 존재하는지에 대한 의문이 생길 수 있다.
그렇다, 이러한 혼합 형태의 알고리즘에 대한 아이디어는 n-step SARSA처럼 샘플을 통한 선택을 할지 혹은 Tree-back up처럼 모든 행동에 대한 예측을 기반으로 한 선택을 할지에 대해 "단계별로 결정할 수 있다"는 것이다. 이를 위해 샘플 기반 선택과 예측 기반 선택의 정도를 'σ(이하 시그마)'기호를 사용하여 정하고 이를 활용하는데, 시그마는 '0'과 '1'사이의 값(0≤σ≤1)이다.
우리는 이러한 알고리즘을 'n-step Q(σ) 알고리즘(이하 큐시그마)'이라고 한다. 우선, 큐시그마 설명에 앞서 n-step SARSA의 반환값 식을 살펴보자.

이러한 식은 순수 샘플링 기반의 반환값 식으로 다시 쓸 수 있는데, 아래와 같다.

이것이 가능함을 토대로 우리는 샘플 기반 타입과 예측 기반 타입의 알고리즘을 자유롭게 넘나 들 수 있다. 이를 설명하기 위해4-step에서 각각의 알고리즘을 비교해보려고 한다. 아래의 도표를 보자(p는 중요도 샘플링을 포함한 전환을 뜻한다).

큐시그마는 n-step SARSA와 Tree-back up을 혼용한 형태로 각 지점마다 시그마 값 조절을 통해 알고리즘을 선택할 수 있다. 이에 대한 갱신식은 다음과 같다.
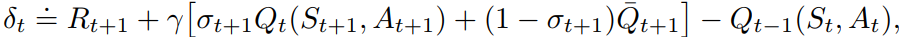
(σ)에 해당하는 값은 샘플 기반의 가치함숫값, (1-σ)에 해당하는 값은 예측 기반의 가치함숫값이고 이러한 식을 활용하면 큐시그마의 반환값 계산이 가능하다.

아래는 큐시그마의 의사 코드이다.

「마무리」
이번 포스트에서 우리는 n-step TD알고리즘에 대해 알아보았다.
n-step TD는 앞선 설명과 같이 MC와 TD의 사이에 위치하는 방법으로서, 각 방법의 장점을 살려 더 나은 성능을 발휘하기 때문에 중요하다.
n-step의 핵심은 n단계를 내다보는 데에 있는데, 이러한 메커니즘은 두 방법의 절충안인 만큼 연산을 위한 딜레이(MC와 같이)와 시간 단계당 수행해야 하는 연산량이 많아지는 것(TD와 같이)과 같은 단점들을 지니고 있다. 하지만, 이 MC와 TD(one-step) 알고리즘에 비해 성능은 더 우수하기 때문에 크게 신경 쓰지 않는다.
n-step TD제어에서는 정책 의존성에 따라 여러 가지 방법으로 나뉘는데, 우선 On-Policy 알고리즘들의 경우 n-step SARSA가 있었다.
n-step SARSA는 단순히 SARSA를 n단계 연장한 것이다. 이를 변형하면 n-step Expected SARSA를 도출할 수 있었고 다만, 마지막 상태에 있어 샘플이 아닌 예측 기반의 갱신식을 활용한다는 차이가 있었다.
반면, Off-Policy방식의 경우는 복잡한데, n-step으로 늘리게 될 경우, MC가 Trajectory기반의 갱신을 진행하는 것과 동일한 방식이 되어버리기 때문에 이전에 등장하였던 중요도 샘플링 방식이 등장한다.
중요도 샘플링을 활용하면 단순하지만 분산이 크기 때문에 이를 사용하지 않고 Off-Policy를 활용하는 방법을 찾았는데, 그것이 Tree-back up 알고리즘이었다. Tree-back up알고리즘의 경우 예측 기반의 알고리즘이었다.
추가적으로 완전한 예측 기반인 Tree-back up알고리즘과 완전한 샘플 기반인 SARSA를 혼합하여 단계별로 선택해 사용하는 알고리즘이 등장하는데 이것이 n-step Q(σ) 알고리즘이었다.
n-step Q(σ) 알고리즘의 경우, σ 값을 통해 샘플사용치에 대한 조정이 가능해 그때그때 알고리즘 연산에 영향을 주었다.
책의 목차에 따른 다음 포스트 내용은 '테이블 방식의 문제 해결법'에 대한 내용이다. 여태껏 우리는 명시적이지 않았으나, 테이블 방식으로 알고리즘을 적용하여 문제를 해결했다. 하지만, 해당 내용이 앞선 포스트에서 다루었던 내용들에 녹아들어있는 개념들에 대한 심도 있는 설명부분이고, 파헤쳐보면 각각의 설명들이 부분마다 다루었던 내용이기 때문에 우선 건너서 그 다음 내용인 '근사화된 함수 방식의 문제해결법(Approximate Solution Methods)' 다룬 이후에 살펴볼 예정이다.
근사화된 함수 방식의 문제해결법은 Continuous Task(연속적 과제)와 같이 상태가 무한히 많아지는 Task에 관해 문제를 풀기 위해, 근사치에 기반해 문제를 푸는 방식인데, 이때 선형 방정식(Linear Approximation)을 활용하기 때문에 함수방식이라고 하는 것이다.
「참고」
Reinforcement Learning, Second Edition : An Introduction
Richard S. Sutton and Andrew G. Barto
https://mitpress.mit.edu/books/reinforcement-learning-second-edition
Reinforcement Learning, Second Edition
The significantly expanded and updated new edition of a widely used text on reinforcement learning, one of the most active research areas in artificial intelligence. Reinforcement learning, one of the most active research areas in artificial intelligence,
mitpress.mit.edu