| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Python Interpreter Lock
- 통합 개발
- 중요도 샘플링
- 오프폴리시
- 파이썬 인터프리터 락
- Meta Learning
- 강화학습
- Importance sampling
- Soft Actor-Critic
- 인터프리터 락
- Concurrency Control
- Off-policy
- Maximazation bias
- Double learning
- Reinforcement Learning
- Actor-Critic
- MAML
- n-step
- Few-shot learning
- Interpreter Lock
- Tree backup
- 전역 인터프리터 락
- Global Interpreter Lock
- 온폴리시
- 도커 텐서보드 연결
- Maximum entropy
- Control variate
- 지속적 개발
- 병행성 제어
- docker tensorboard
- Today
- Total
HakuCode na matata
하쿠's 강화학습 :: [Ch. II] Multi-armed Bandits 본문
하쿠's 강화학습 :: [Ch. II] Multi-armed Bandits
@tai_haku 2020. 8. 30. 08:56포스팅에 앞서 이 게시글은 Reference의 contents를 review하는 글임을 밝힌다.
「Multi-armed Bandits 문제란?」
'Multi-armed Bandits(이하 MAB)'문제는 확률이론에서 등장하는 문제로 카지노 슬롯머신을 통한 도박을 진행함에 있어서,
어떻게 하면 최대 수익(보상)을 얻을 수 있는가에 대한 문제이다.

이는 강화학습과 목표와 문제 해결이 유사하기 때문에, 강화학습 알고리즘을 공부할 때 등장하는 고전적인 문제이다. 이번 장에서는 이러한 MAB문제를 통해서 강화학습의 여러 기초 개념에 대해 알아볼 것이다.
알아볼 개념들은 다음과 같다.
① 탐험-이용(Exploration & Exploitation) 알고리즘
② 증분식을 통한 학습
③ 바람직한 초기 값 설정
④ 행동선택 알고리즘(UCB, Gradient bandit)
⑤ 연관적 과제(연관성)
강화학습과 다른 기계학습의 가장 큰 차이점은 스스로의 경험을 통해서 점진적으로 수행력을 강화시키는 부분이라고 할 수 있는데, 이것을 가능하게 하는 것이 탐험-이용(Exploration & Exploitation) 알고리즘이다.
이어서, 제한된 컴퓨팅 리소스 내에서 여러 시행을 거쳐 점진적으로 성능이 개선되는 강화학습 특성상 요구되는 학습 방식인 증분식을 통한 학습과 학습에 도움을 주는 바람직한 초깃값 설정, 최적의 행동선택에 있어서의 여러 방법론인 UCB 알고리즘과 Gradient bandit 알고리즘, 마지막으로 MAB문제와 일반 강화학습 문제의 차이점인 연관성의 개념까지 알아볼 예정이다.
그럼 지금부터 차근히 설명을 따라가보자.
「강화학습의 훈련 방식에 있어서의 차별점」
이전 장에서도 지도/비지도 학습과의 차이를 간결하게 설명한 바 있다.
추가적으로 구별되는 점은 '훈련에 대한 피드백(보상)의 작용에 있어서의 성질 차이'이다.
우선, 훈련 데이터가 요구되는 지도 학습과 비교해보자면,
지도학습은 훈련 데이터를 '행동지시'에 사용하지만,
강화학습은 훈련 데이터를 '행동평가'에 사용한다는 것이다.
행동지시는 실제로 행동한 선택지와는 별개로 작용한다(정해진 답이 있고, 그것이 곧 목표).
내가 어떠한 행동을 했는지 무관하게, 특정한 행동을 해야 하고 이외의 선택은 틀린 것이다.

행동평가는 실제로 행동한 선택지에 대해서 작용한다(정해진 답이 없고, 목표만 따로 존재).
내가 실행한 행동이 최적으로부터 얼마나 차이가 있는지를 평가하여 보상을 받는다.
정해진 답이 없이 출발하는 강화학습은 행동평가를 통해 학습을 하는 방식을 채택함으로써, 행동을 선택할 때, 현시점에서의 최선을 선택하는 방법(이용-Exploitation)과 미래의 잠재성(아직 발견하지 못한 최선)을 선택하는 방법(탐험-Exploration) 중에서 선택하게 된다.
「MAB에서의 탐험-이용(Exploration-Exploitation) 알고리즘」
앞서 말한 행동평가를 하기 위해선, 그 가치를 파악하는 것이 우선이다.
여러 시행에서의 특정 행동 a을 통해 얻어지는 보상의 평균, 앞으로 우리는 그것을 a의 행동가치함수라고 할 것이다.
다음 행동가치함수식을 보자.

t는 단위시간이다(현재를 가리킨다).
At는 현재 수행한 행동이다(여기서는 a이다).
Rt는 At로 얻어지는 보상이다.
E는 기댓값(여기서는 평균치)이다.
수식의 연산 결과인 q(a)는 행동 At(여기서는 a)를 수행함으로써 얻어지는 보상의 기댓값(평균)을 말하고, 이것이 MAB에서의 행동가치함수이다. 하지만, 여기서 나타난 q*(a)는 우리가 각 행동가치에 정확하게 알고있다고 가정할 때의 최적의 행동가치 함숫값를 의미한다.
강화학습에서는 이러한 정확한 최적의 행동가치 값을 모르는 상태에서 평가와 개선의 방식으로 점차 나아가야 한다.
따라서, 우리는 행동가치 값을 평가하게 되는데 단위시간 t에서의 행동 a의 평가된 행동가치 값을 qt(a)라고 한다.
이는 우리가 평가한 행동가치 값으로, 우리의 목표는 이 qt(a)값을 q*(a)에 근접하게(최적화)하는데 있다(수식은 아래와 같다).
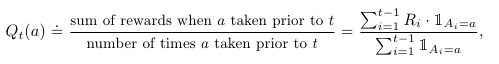
식 <1Ai=a>는 '행동 a를 선택했을 때'를 말한다. 따라서 이 수식을 그대로 해석하면, 이전 시행까지 행동 a를 선택했을 때의 모든 보상의 합을 이전 시행 횟수로 나눈 것이다. 다시 말해, 행동 a에 대한 평균 보상이라고 할 수 있다.
이를 숙지하고 아래의 슬롯머신을 함께 보자.

우리는 두 대의 슬롯머신 중 1) 둘 다 선택할 수,2) 좌측을 선택할 수, 3) 우측을 선택할 수, 4) 아무것도 선택하지 않을 수가 있다. 선택 시에는 확률적으로 금전적 보상을 받게 되고, 어떤 선택을 하든 우리는 슬롯머신을 활용해 제일 많은 금전적 보상을 획득하는 것이 목표이다.
처음에는 어떤 슬롯이 돈이 잘 나오는지 몰라, 무작위로 선택하면서 게임을 할 것이다.
허나, 점차 게임이 진행될수록 각 선택(=행동)의 가치 값을 계산하여 비교적 수익이 날 확률이 높은 쪽의 기계를 선택하여 게임을 할 것이다.

이렇게, 높은 가치를 얻을 것으로 예상되는 행동을 선택하는 것을 '이용(Exploitation)'이라고 하고,
이용만을 활용하는 알고리즘을 '그리디 알고리즘(Greedy algorithm)'이라고 한다.
이런 식으로 게임을 계속 진행해가다 보면 정해진 수익률을 벗어나지 못하게 될 때가 있다(오히려 손해만 볼 수도 있다).
이럴 때, 우리는 더 좋은 선택 방법이 있을까? 하고 여지껏 평가된 최적의 선택이 아닌 다른 선택지로 눈을 돌려본다.
시도해본 결과, 의외로 성과가 기존 방법을 따른 성과보다 우수했다..!
그렇다, 사실은 우리가 기존에 최적이라고 여기던 수는 그렇지 않았던 것이다. 실은 목표점은 예상이 빗나간 곳에 존재했다.
우리는 다른 방향을 선택함으로써 최적의 수에 한층 더 가까워졌다.

이렇게, 현재의 최적 수를 벗어나 다른 선택을 해보는 것을 '탐험(Exploration)'이라고 한다.
허나, 이런 식으로 탐험의 선택이 주를 이루게 되면 기존의 수익률도 유지하기가 힘들어질 가능성이 있다.
따라서, 강화학습에서는 최종적으로 이 둘을 균형 있게 활용하여 선택하는 방식을 채택하는데,
이것이 '탐험-이용(Exploration-Exploitation) 알고리즘'이다.

어떤 특정한 경우에라도, '탐험'이 나은 선택인지, '이용'이 나은 선택인지의 여부는 추정치의 정확한 값, 불확실성, 남은 단계의 수에 따라 복잡한 방식으로 결정된다(특정할 수 없다).
실질적으로 이용방식만을 활용하는 그리디 알고리즘은 보상의 노이즈(noise)와 편차(bias)가 적을수록, 그 효과가 잘 드러난다.
허나, 우리가 직면할 과제(실제 세계의 문제)들은 그런 경우가 드물기 때문에, 이 둘의 밸런싱(balancing)이 중요하다.
탐험-이용을 사용하는 알고리즘 중에는 '엡실론-그리디 알고리즘(E(Epsilon)-greedy algorithm)'이 있다.

Epsilon(이하 E)은 불확실성으로, 탐험을 활용한(랜덤 하게) 선택을 할 확률이다.
나머지 1-Epsilon의 확률은 이용을 활용한 선택을 할 확률이다.
이런 식으로, 탐험과 이용을 번갈아가며 선택할 시에 어느 한쪽에 치우친 선택을 했을 때보다,
결과적으로 우수한 성능을 보인다.

「증분 형태의 학습 진행」
강화학습은 얻어진 경험을 토대로 점진적인 개선을 통해 최적화로 나아가는 학습방식이다.
그러한 학습을 하기 위해, 각 행동들을 통해 얻은 보상의 평균값을 기준으로 연산을 진행할 것이다.

어떤 값을 기준으로 "점진적이다"라는 것은 결국 지금보다 더 나은 것, 즉 과거의 데이터를 종합하여 나아간다는 뜻인데
제한된 컴퓨터 메모리 상에서 이러한 계산을 어떻게 수행하는지에 대해 알아보도록 한다. 다음 식을 보자.

각각의 Rn은 n차 시기에서 행동 a를 선택했을 때의 즉각보상이다.
분모의 n-1은 전체 시행 횟수로 과거까지의 시행 횟수를 말한다.
qn은 현재 상태에서의 행동 a에 대한 행동가치함수이다.
이 값들을 모두 저장하고 필요시, 연산을 그때그때 수행한다는 것은 매우 비효율적인 방법이다.
더군다나, 시간에 따라 지속적으로 행동이 수행될 경우 메모리 사용량도 점차 증가한다.
따라서, 우리는 증분(增分)식을 활용할 것이다. 아래의 식을 같이 보자.

마지막 줄을 해석하면, 현재 행동에 대한 즉각보상과 이전 시행까지의 행동가치함수의 차에 시행 횟수만큼,
scaling 하여 현재 행동가치함수에 합산하면 최신의(현재까지의) 행동가치함수를 생성할 수 있게 된다.
여기서 scaling의 인자로 사용되는 1/n을 'Step size'라고 부를 것이다.
다른 기계학습에서의 'Learning rate'라고 생각하면 편하다.
여기서 잠깐 둘의 차이에 대해 짚고넘어가자면, 변수(Step size = Variable)냐 상수(Learning rate = Constant)냐의 차이인데, 이는 강화학습의 문제 크기에 따라 달려있다.
유한(finite)의 시행 횟수를 가진 구현에서는 있는 식 그대로 사용해도 무리가 없다.
하지만, 그렇지 않고 무한(infinite)의 시행 횟수를 가진 구현에서는 상수 값의 Step size를 활용하여야 하는데,
이 경우, Learning rate와 완전히 같은 기능을 한다. 그리고 이렇게 상수 값의 Step size를 사용할 경우는 최신 값 반영 시,
그 영향력이 과거의 값보다 크게 작용하기 때문에, 최신 결과에 더욱 가중치를 두게 된다
(왜냐하면 시행이 늘어날수록 커지는 변수 n의 특성상, 나중에 한 경험일수록 나눗셈에 사용되는 분모 n의 크기가 커져,
결과적으로 Step size가 작아지기 때문).

결국 Step size는 '변화에 대한 반영 정도'를 정하는 것으로, 이 값이 클수록 변화를 크게 반영한다는 뜻이다.

추가적으로 이 식에서 우리는 행동을 통해 얻어진 보상을 통해 현재 상태에서 나아가야 할 방향과 크기 정보(벡터 값 정보)를 알 수 있게 되는데, 이때 보상을 우리가 나아갈 목표(Target)라고 하고, 벡터 값 정보(목표와 현재 상태 간의 차이)를 에러([Target - OldEstimate])라고 표현한다(에러는 딥러닝에서의 손실 함숫값이라고 이해하면 편하다).
여지껏 설명한 작업을 프로그램 상의 의사코드로 나타내면 아래와 같이 구현할 수 있다.

「바람직한 초깃값 설정」
초깃값 설정은 보다 쉽게 학습자(기계)에게 목표에 대한 선행지식을 주입할 수 있다는 장점이 있다.
또한, 탐험을 더욱이 선택하도록 고취시킬 수도 있다. 우리는 이렇게 탐험에 대한 선택을 장려하는 초깃값을
'바람직한 초깃값(Optimistic initial values)'이라고 한다.
그러나, 이러한 테크닉은 비정류(非整流) 즉, 목표나 해저드(장애물)가 상시 변하는 동적 환경에서는 잘 들어맞지 않는다
(아래와 같은 장애물이 동적인 환경에서는 적절하지 못하다).

본질적으로 수행 초기에 제한된, 한시적인 탐험 장려법이기 때문에, 추후 환경이 바뀌었을 때 이에 대한 새 탐험이 필요하나, 이를 지원할 수 없다. 이처럼 제한적 사용과 효과에 대한 비판이 꽤나 있으나, 실전에서 유용하게 쓰이는 방법 중 하나라고 기억하면 좋겠다.

「Upper-Confidence-Bound(UCB) 행동 선택법」
불확실성이 존재하는 한, 탐험은 필수 요소라고 하였다.
이것을 증명하기 위해, 현재의 최선을 선택하는 Greedy 알고리즘보다 약간의 탐험을 가미시킨 E-greedy 알고리즘이 더 우수하다는 결과도
앞서 살펴보았다.
그렇지만 E-greedy알고리즘 역시 랜덤 하게 다른 행동을 선택할 뿐,
최선이 아닌 선택 중 어떤 행동이 좀 더 우리의 목표에 가깝게 만들어줄 지에 대한 논의는 없었다.
이렇게, 다른 선택 중에서도 차선의 선택을 하자는 아이디어를 가능케하는 방법 중 하나가 'Upper-Confidence-Bound(이하 UCB) 알고리즘'이다.
UCB의 아이디어는 간단하다. 바로 행동의 잠재성(potential)을 선호도(preference)로서 측정하는 것인데, 다음 식을 보도록 하자.

상수 c(c>0)는 탐험 정도이고,
Nt(a)는 지금까지 행동 a를 선택한 횟수,
lnt는 자연로그 값이다.
제곱근 안에 있는 요소들은, 행동 a에 대한 불확실성의 평가이다.
따라서, 전체 수식을 풀이해보면, 여지껏 선택한 횟수가 적은 행동을 선택하는 방식임을 알 수 있다.

그러나, 이러한 UCB알고리즘은 이전 구절(바람직한 초깃값 설정)과 동일하게 비정류환경에는 적합하지 않다
(목표가 바뀌면 새로운 탐험이 요구되기 때문).
또한, 도메인 사이즈(상태를 나타내는 값의 개수)가 비대해지면 현실적으로 적용(연산)에 어려움이 있기에 잘 사용하지 않는다.
「Gradient Bandit 알고리즘」
앞서 살펴본 UCB 알고리즘의 선호도 측정 기준이 잠재성(potential)이었다면,
이번에 살펴볼 Gradient Bandit 알고리즘의 선호도 측정 기준은 중요도(importance)에 있다.
이는 행동이 가져다 줄 보상으로 해석되지 않고, 그 행동이 얼마나 중요한가를 나타내는 지표이다.
또한, 이 선호도는 다른 행동들과의 상대적인 지표이다. 선호도는 Ht(a)로 표기한다. 다음 식을 보자.

수식의 가운데 있는 식은 Softmax 식이다.
Softmax 식은 다음과 같이 정의하는데, 그 해석은 전체 행동들의 특정 도메인(x)에 대한 결과를 합한 값(∑f(n))과
행동 a의 특정 도메인(x)에 대한 결과(f(a))간의 상대적 비율을 계산한다.
쉽게 말해, 전체 10개 중 내가 3개를 가지고 있으면 Softmax 값은 0.3이다(전체 대비 a의 비율).

돌아와서, 전체 중 행동 a를 선택할 비율이 선호도인데, 그렇다면 선호도는 어떻게 설정하는가? 가 의문으로 남게 된다. 초기에는 모든 행동이 같은 선호도를 갖게 된다(확률적 경사 하강법 기반). 여러 번의 시행을 거쳐 선호도는 아래와 같은 식으로 갱신된다.

(이 수식에 한해 선택된 행동 a는 At로, 선택되지 않은 행동들은 a로 생각해보자.)
첫 번째 줄을 들여다보면, 이 식은 선택된 행동 At에 대한 선호도를 산출하는 식이다. 보상 간 차이에 곱해지는 인수 alpha는 Step size이고, 현재 보상 Rt에서 차감되는 보상값 bar {Rt}은 현재까지의 평균 보상 값(이하 기저보상)이다.
즉, 이 둘의 값의 차이는 기저보상으로부터 현재 보상이 얼마나 차이가 있는가를 알려주는 인수이다. 여기에 행동 At의 비율을 곱하여 기존 선호도에 합산하면 선택된 행동의 선호도가 산출된다.
반면, 두 번째 줄을 들여다보면, 이 식은 선택되지 않은 나머지 행동들 a에 대한 선호도를 산출하는 식이다. 동일한 방식으로 기저보상과 현재보상의 차이에 Step size와 나머지 행동들에 대한 a의 비율을 곱하여 이번에는 기존 선호도에서 차감하는 방식으로 계산한다.
이런 식으로 즉각보상과 기저보상간 차이를 활용하여 선택된 행동에 대해서는 차이 벡터 값의 방향으로 증감시키고,
나머지 행동들에 대해서 그 반대 방향으로 증감시키는 방법을 그레디언트 밴딧(Gradient Bandit) 알고리즘이라고 한다.
또한, 이렇게 선호도를 계산하여 각 상태별 각 행동에 대한 선호도를 계산해놓은 것을 '정책(Policy)'라고 한다.
이전 포스트에서 간략히 설명하였듯이, 정책은 행동지침이다. 각 상태별 행동들에 대한 선호도가 맵핑되어있고,
이를 활용하여 행동을 선택하게 된다.
다음 그래프는 그레디언트 밴딧 알고리즘의 효과를 그래프로 나타낸 것이다.

「연관적 과제」
앞에서 알아보았던 과제들 모두, 비연관적 과제들이었다.
비연관적 과제란,

말 그대로 여러 상태가 연관되지 않고 오로지 관측 가능한 상태와 최선의 행동이 각각 하나씩인 경우를 말한다.
여지껏, 각 슬롯의 레버들을 당김에 있어서 이전의 성공한 시행 횟수 말고는 관측 가능한 상태가 없었다.
이러한 과제에서 학습자(기계)는 환경특성(정류, 비정류)에 무관하게 각 상황별 최선의 행동만을 학습하려고 노력한다.

그러나, 일반적인 강화학습의 문제(실세계의 문제)에서는 다양한 상황(관측 가능한 상태)이 있기 때문에,
학습의 목표는 정책(여러 상태를 조합한 복합 상태에서의 행동지침)을 학습하는 것이다.

이러한 문제가 바로 연관적 과제이다.
지금부터는 연관적 과제에 대해 다뤄보려고 한다. 연관적 과제의 예시는 쉽다.
지금부터 레버를 돌리면 보상을 받을 수 있다는 사실과 관련된 단서 하나를 추가해보겠다.
보상을 얻을 수 있는 직전 상태의 슬롯머신에는 불빛이 들어온다(이것은 행동가치와는 다른 단순한 단서이다).
이렇게 되면, 비록 기존에 관측하던 상태 값으로 미루어볼 때, 목표 도달이 가능하지 않은 상태더라도 우리는 불빛의 관측을 통해 목표 도달 가능성을 엿보고 해당 상태에서 기존에 취하던 행동과 다른 행동을 취할 수 있게 된다(쉽게 말해, 관측 가능한 상태가 2가지가 된다는 뜻).
연관적 과제의 특징은 비연관적과제와 같이 즉각보상에 영향을 미칠 뿐만 아니라, 조금 전과 같이 다음 상태에도 영향을 미친다는 것이다(다른 행동을 선택함으로써 다른 다음 상태를 갖게 됨).
우리는 이러한 연관적 과제를 Associative search task 또는 Contextual bandits라고 부른다.
이제까지의 Bandits문제는 실질적인 강화학습의 문제라고 보기 어려웠으나, 이런 식으로 연관적 과제의 성격을 띠게 되면 비로소 진정한 강화학습문제라고 말할 수 있는 것이다.
우리는 이러한 연관적 과제(다음 상태에 영향을 끼치는)에 대해 다음 포스트에서 이어서 알아볼 예정이다.
「마무리」
우리는 이번 포스트에서 강화학습에서의 핵심 알고리즘인 탐험-이용 알고리즘과 증분식을 통한 학습법,
학습 성능을 향상하기 위한 테크닉(초깃값 설정 및 행동 결정 알고리즘) 들을 살펴보았다.
다음 포스트에서는 강화학습문제성립에 있어서의 기본 토대인 Markov Decision Process(이하 MDP) 속성에 대해 알아보려고 한다.
「참고」
Reinforcement Learning, Second Edition : An Introduction
Richard S. Sutton and Andrew G. Barto
https://mitpress.mit.edu/books/reinforcement-learning-second-edition
Reinforcement Learning, Second Edition
The significantly expanded and updated new edition of a widely used text on reinforcement learning, one of the most active research areas in artificial intelligence. Reinforcement learning, one of the most active research areas in artificial intelligence,
mitpress.mit.edu
'Machine Learning > Reinforcement Learning' 카테고리의 다른 글
| 하쿠's 강화학습 :: [Ch. VI] Temporal-Difference Learning (0) | 2020.10.13 |
|---|---|
| 하쿠's 강화학습 :: [Ch. V] Monte Carlo Methods (2) | 2020.10.04 |
| 하쿠's 강화학습 :: [Ch. IV] Dynamic Programming (0) | 2020.09.27 |
| 하쿠's 강화학습 :: [Ch. III] Finite Markov Decision Process (2) | 2020.09.20 |
| 하쿠's 강화학습 :: [Ch. I] Introduction (0) | 2020.08.12 |




